Room 329, North Building, School of Mathematics, Tongji University
2025年8月3-8日, 同济大学数学科学学院
2025.08.03-08, School of Mathematics, Tongji University
Registration is now closed.
In the week after the summer school there will be a Workshop and Summer School on Hyperplane Arrangements and Related Topics in Tongji University.
胡昊宇Haoyu Hu (Nanjing University)
Laurentiu Maxim (University of Wisconsin–Madison)
秦翊宸Yichen Qin (Humboldt-Universität zu Berlin)
许大昕Daxin Xu (Morningside Center of Mathematics)
| Sun 08.03 |
Mon 08.04 |
Tue 08.05 |
Wed 08.06 |
Thu 08.07 |
Fri 08.08 |
|
|---|---|---|---|---|---|---|
| 8:30-10:00 | Registration | Hu1 | Hu2 | Hu3 | Hu4 | Free Discussion |
| 10:30-12:00 | Xu1 | Xu2 | Xu3 | Xu4 | ||
| 14:00-15:30 | Qin1 | Maxim2 | Qin3 | Maxim4 | ||
| 16:00-17:30 | Maxim1 | Qin2 | Maxim3 | Qin4 | ||
| 18:30 | Banquet |
Haoyu Hu: Introduction to D-modules
The series of lectures is divided into two parts. In the first part, we discuss the fundamental notions of algebraic D-modules theory, including six functors and characteristic varieties. In the second part, we focus on the Riemann-Hilbert correspondence for regular meromorphic connections.
Laurentiu Maxim: Singularities via mixed Hodge modules
I will start by giving a brief introduction to the theory of mixed Hodge modules. I will then proceed to show how this theory can be used to investigate singularities of complex algebraic varieties, especially of hypersurfaces.
Yichen Qin: Mixed Hodge modules
The aim of this lecture series is to introduce Morihiko Saito's theory of mixed Hodge modules. We will first recall some background on variations of mixed Hodge structures, D-modules, and perverse sheaves. We will then define the category of mixed Hodge modules and discuss some important results, such as the decomposition theorem and stability under the 6-functor formalism.
Daxin Xu : Introduction to arithmetic D-modules
The rigid cohomology is a Weil cohomology for varieties over field of positive characteristic. The theory of arithmetic D-module is the 6-functor formalism for the rigid cohomology. This theory is built on the works of Berthelot, Caro, Abe and others. In this course, I will explain some constructions and results in this theory.
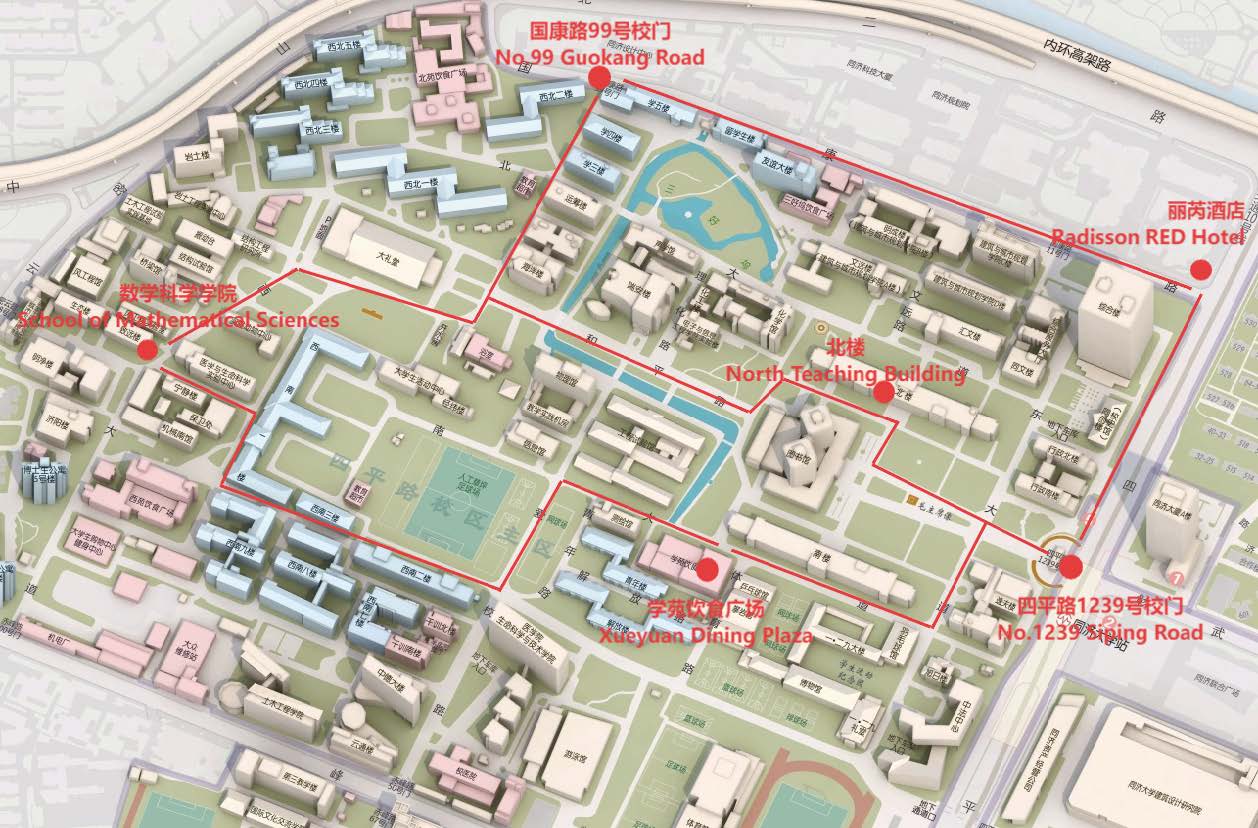
同济大学数学科学学院, 北楼329教室
Room 329, North Building, School of Mathematics, Tongji University
金方舟, 李灵光, 林胤榜, 张希平, 张子立, 朱子文
组织单位：同济大学数学科学学院
资助项目：科技部国家重点研发计划项目2021YFA1001400、国家自然科学基金12471014