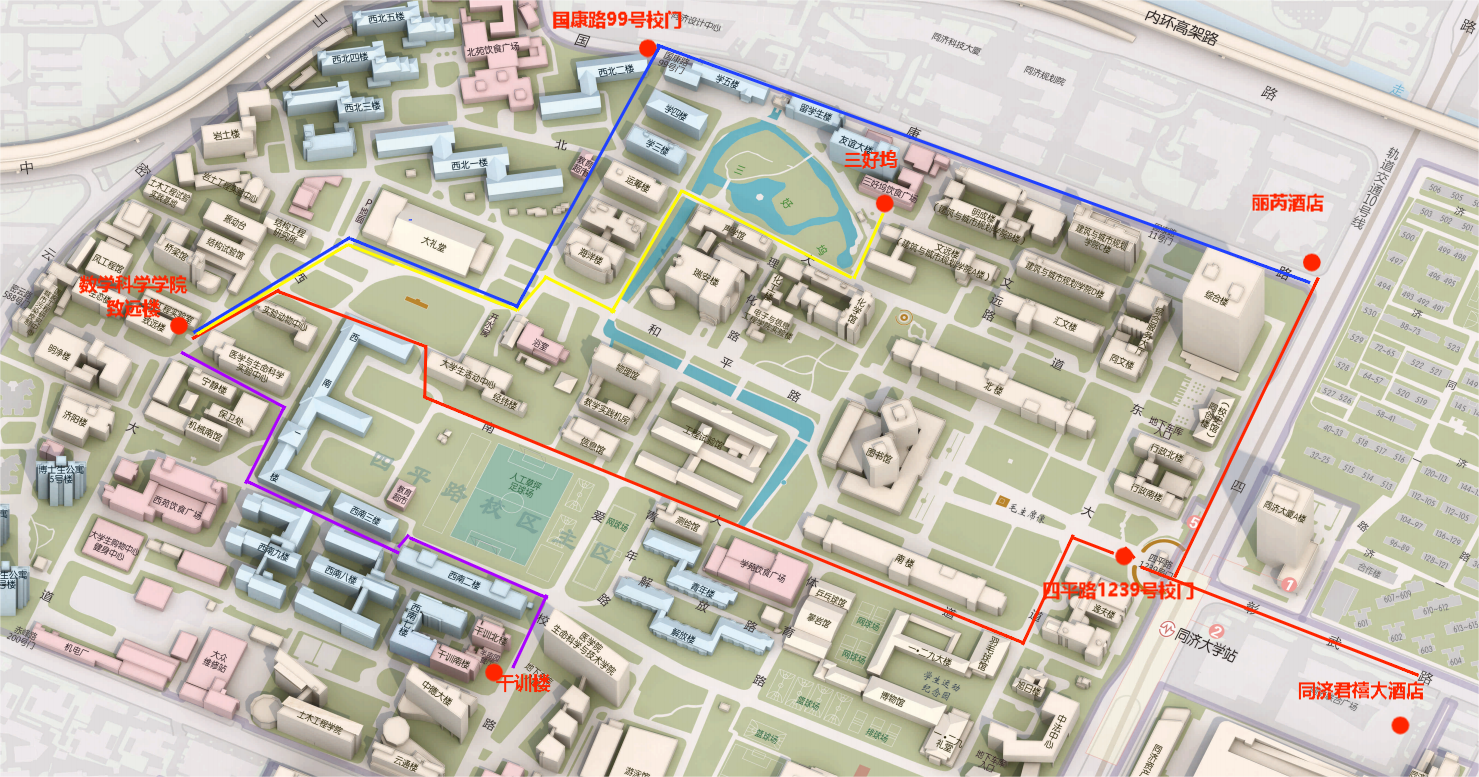
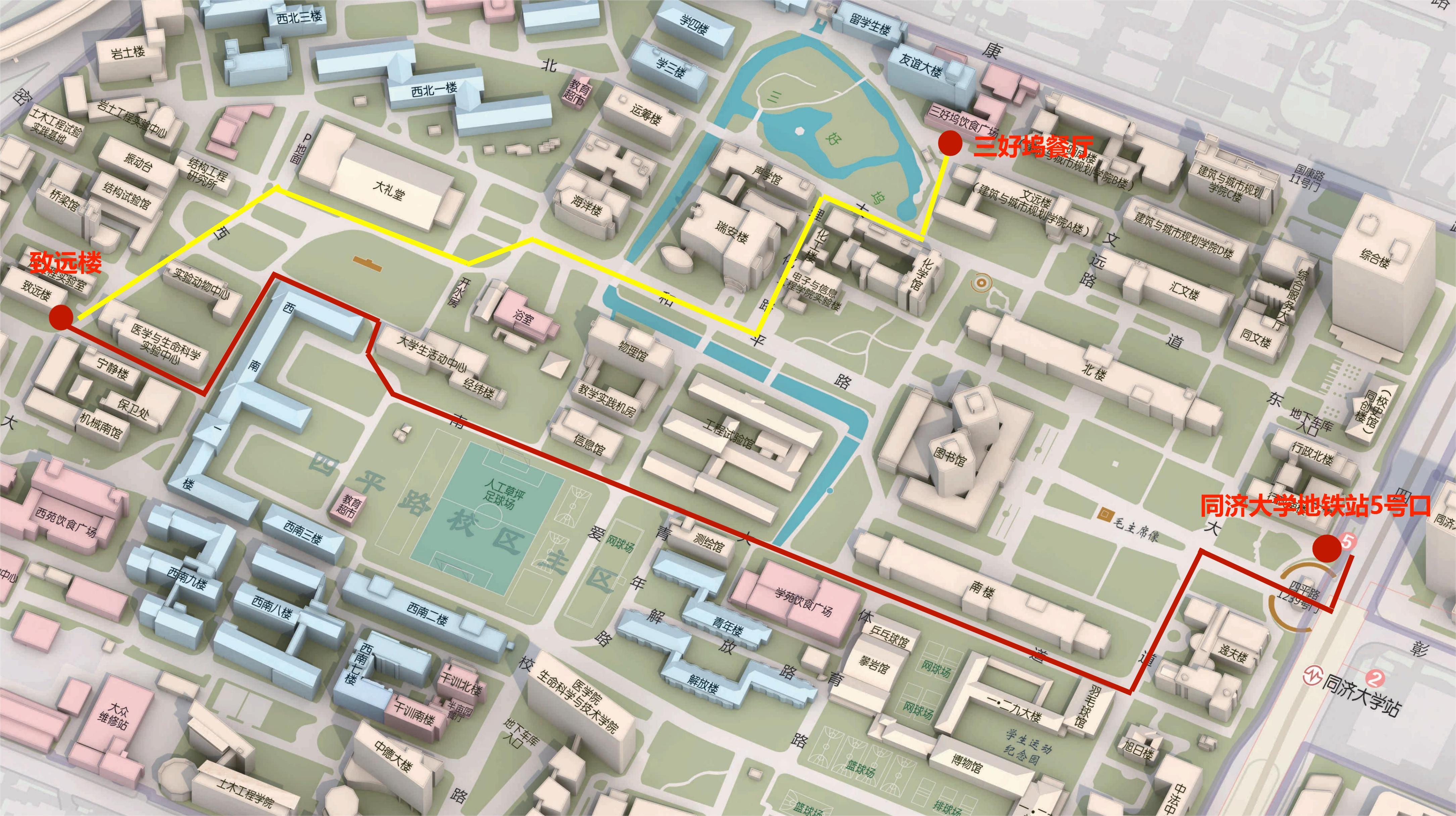

2024年5月24-27日, 同济大学数学科学学院
陈苗芬(复旦大学)
胡昊宇(南京大学)
胡晓文(大湾区大学)
刘一峰(浙江大学)
谢恒(中山大学)
许大昕(中国科学院晨兴数学中心)
闫旗军(北京雁栖湖应用数学研究院)
赵和耳(哈尔滨工业大学)
5月24日
报到
5月25日
9:00-10:00 刘一峰
合影
10:30-11:30 胡昊宇
午餐
14:00-15:00 陈苗芬
15:20-16:20 许大昕
16:40-17:40 闫旗军
晚宴
5月26日
8:30-9:30 赵和耳
9:45-10:45 谢恒
11:00-12:00 胡晓文
午餐
5月27日
自由讨论
刘一峰:Theta lifts in Selmer groups
In this talk, we study generating series on unitary Shimura varieties valued in Selmer groups. We show its modularity under some natural hypothesis, based on which we construct theta lifts valued in Selmer groups. Finally, we compute the p-adic height of our Selmer theta lifts, obtaining a formula known as the p-adic arithmetic inner product formula, which can be regarded as a higher dimensional generalization of Perrin-Riou's p-adic Gross-Zagier formula. This is a joint work with Daniel Disegni.
胡昊宇:Semi-continuity of conductors
In this talk, I will introduce a recent progress on the semi-continuity of largest Abbes-Saito ramification slopes for étale sheaves on higher relative dimensional varieties of positive characteristic. It is a higher dimensional analogue of André's semi-continuity result for Poincaré-Katz rank of meromorphic connections on complex relative curves, and it has applications on the boundedness Betti numbers of étale sheaves with bounded wild ramifications. This is a joint work with Jean-Baptiste Teyssier.
陈苗芬:Extensions of Vector bundles and Non-emptiness of Newton stratification in p-adic Hodge theory
A p-adic period domain is an open subspace inside the rigid analytic p-adic flag varieties introduced by Rapoport and Zink which interpolates a family of crystalline representations. Newton stratification is a stratification on the rigid analytic p-adic flag varieties which has p-adic period domain as its unique open stratum. In this talk, we will study the non-emptiness of a Newton stratum which is closely related to the classification of extensions of vector bundles on the Fargues-Fontaine curve. It's a joint work with Jilong Tong.
许大昕:Drinfeld Lemma for F-isocrystals
Drinfeld's lemma for l-adic local systems is a fundamental result in arithmetic geometry. It plays an important role in the Langlands correspondence for a reductive group over the function field of a curve over a finite field, pioneered by Drinfeld for GL_2 and subsequently extended by L. Lafforgue and then V. Lafforgue. In this talk, we will discuss Drinfeld's lemma for p-adic local systems: overconvergent/convergent F-isocrystals. This is based on a joint work with Kiran Kedlaya.
闫旗军:On Certain Reductions of Frobenius Period Maps for Shimura Varieties
Given a Shimura variety of Hodge type (which, for this talk, can be considered as the moduli space of abelian varieties), the construction of Frobenius period maps for the integral model is straightforward and relatively simple. However, certain types of reductions are less so. In this talk, I will describe some of these reductions and derive a loop group valued period map for the special fiber of the Shimura variety.
赵和耳:Tame covers and Kummer log flat torsors
(joint with J. Gillibert) Let X be a regular scheme, D a normal crossing divisor on X, and U the complement of D. We endow X with the canonical log structure associated to D. Let G be a finite flat group scheme (not commutative in general) over X. We discuss the relations among tame G-covers of X relative to D, fppf G-torsors over U, and Kummer log flat G-torsors over X.
谢恒:Pushforward in Hermitian K-theory via Grothendieck's residue complex
Hermitian K-theory, a cohomology theory, has found interesting applications in recent works. Through a series of works by Asok, Fasel, and Srinivas, the obstruction class for splitting algebraic vector bundles is shown to reside in Hermitian K-theory under certain conditions. Moreover, Hermitian K-theory aids in understanding an unsolved problem on the composition of quadratic forms posed by Hurwitz in 1898. However, not many computations have been done in Hermitian K-theory. Pushforward is a powerful computational tool in cohomology theory. Recently, we developed pushforward in Hermitian K-theory via Grothendieck's residue complex. Additionally, we have proven the base change, projection, and excess intersection formulas. These tools allow us to compute the Hermitian K-theory of Grassmannians, leading to a special class of Young diagrams that we call buffalo-check Young diagrams. This is joint work with Tao Huang.
胡晓文:On the rationality of dlog A^1-zeta functions
For smooth proper schemes over a finite field k, Bilu, Ho, Srinivasan, Vogt, and Wickelgren introduced the dlog A^1-zeta function with coefficients in the Grothendieck-Witt ring of k, enriching the dlog of the classical Weil zeta function. They introduced the notion of dlog rationality, and showed this property for simple cellular schemes. In this talk, we will review their theory and show that the dlog A^1-zeta functions are always rational, but not necessarily dlog rational.
同济大学数学科学学院,致远楼108报告厅



金方舟, 李灵光, 林胤榜, 张希平, 张子立, 朱子文
组织单位:同济大学数学科学学院
资助项目:科技部国家重点研发计划项目2021YFA1001400、国家自然科学基金青年项目12101455