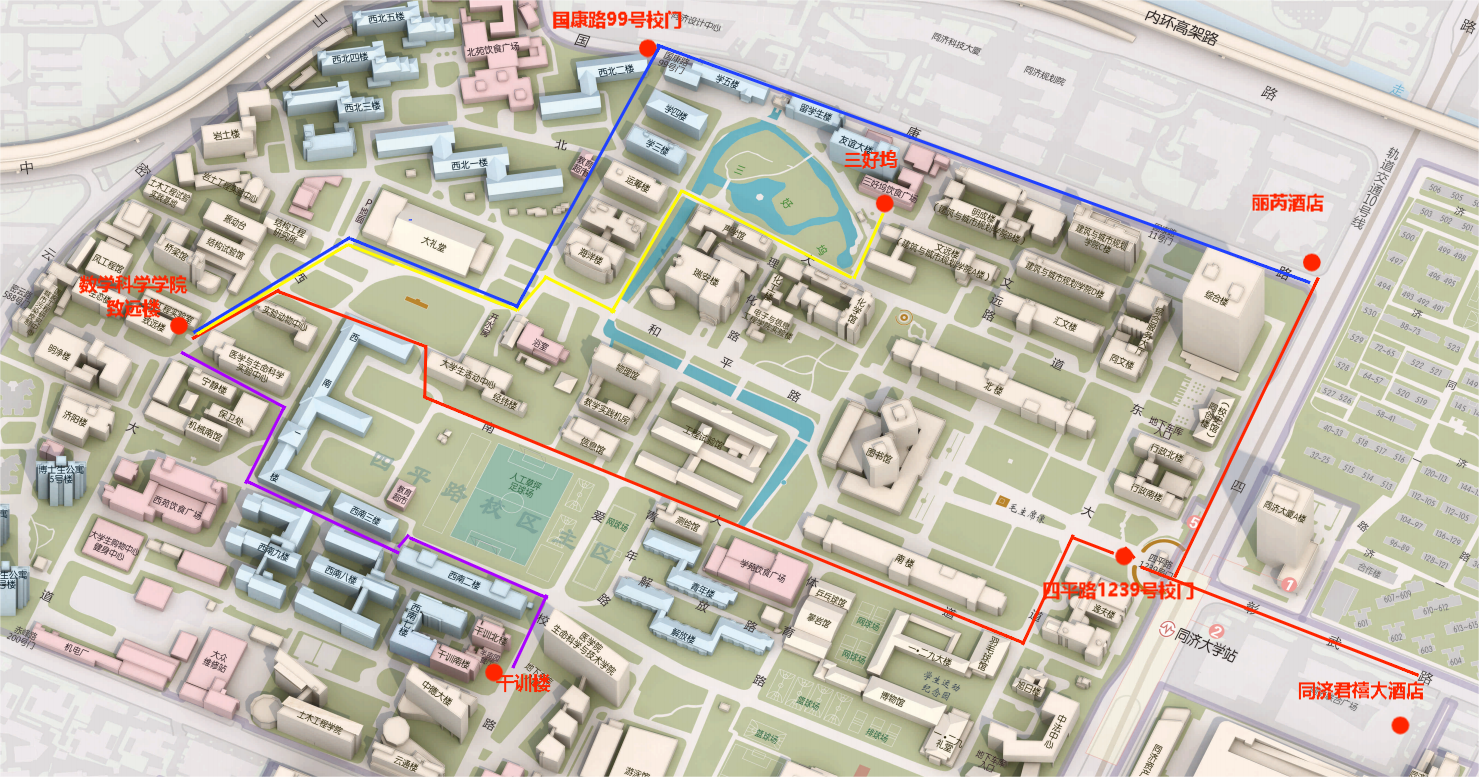
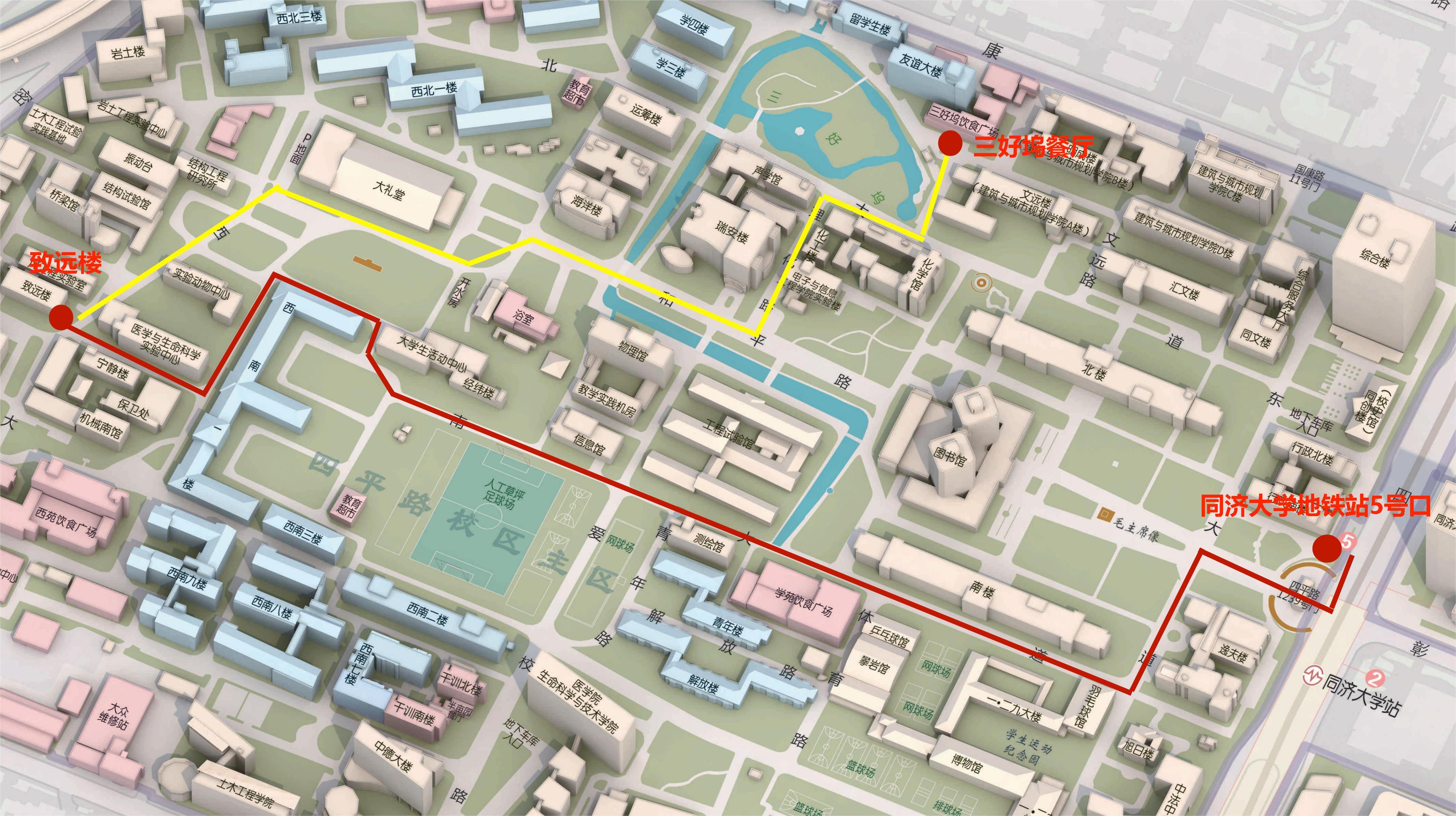

2023年5月26-29日, 同济大学数学科学学院
蔡金星(北京大学)
曹晋(清华大学)
陈猛(复旦大学)
韩京俊(复旦大学)
李起峰(山东大学)
孙笑涛(天津大学)
谈胜利(华东师范大学)
田志宇(北京大学)
杨南君(北京雁栖湖应用数学研究院)
张鼎新(清华大学)
周杨(复旦大学)
左康(武汉大学)
5月26日
报到
5月27日
8:20-8:30 开幕式
8:30-9:30 左康(武汉大学)
9:45-10:45 孙笑涛(天津大学)
合影
11:00-12:00 李起峰(山东大学)
午餐
14:00-15:00 谈胜利(华东师范大学)
15:15-16:30 韩京俊(复旦大学)
16:45-17:45 周杨(复旦大学)
晚宴
5月28日
8:30-9:30 陈猛(复旦大学)
9:45-10:45 蔡金星(北京大学)
11:00-12:00 田志宇(北京大学)
午餐
14:00-15:00 杨南君(北京雁栖湖应用数学研究院)
15:15-16:30 曹晋(清华大学)
16:45-17:45 张鼎新(清华大学)
晚餐
5月29日
自由讨论
蔡金星(北京大学):Involutions of irregular surfaces and their induced actions in cohomology
Let S be a complex nonsingular minimal irregular projective surface. An involution σ of S is said of regular type, if σ^*=-id on H^0(X,Ω^1_S); otherwise, it is said of irregular type. In this talk, the classification for surfaces with an involution of irregular type acting trivially on H^2(S,Q) is given. We also raise some questions on the classification for surfaces with an involution of regular type acting trivially on H^2(S,Q).
曹晋(清华大学):Gauss-Manin connection in disguise - Quasi Jacobi forms
The project of Gauss-Manin connection in disguise aims at giving a systematic way of understanding classical modular forms by studying moduli spaces with extra data. In this talk, I will describe recent joint work with R. V. Loyola and H. Movasati for the understanding of
quasi Jacobi forms.
陈猛(复旦大学):三维代数簇的最小体积猜想及分类工作的新进展
此综合报告主要介绍一般型三维代数簇的最小体积猜想的研究进展和三维簇分类工作方面的一些新的研究方法。
韩京俊(复旦大学):On termination of the flips and enc singularities
In this talk, I will introduce the so-called "exceptionally non-canonical singularities".Although being noncanonical, such pairs are expected to have nice properties. In particular, it is predicted that the set of minimal log discrepancies (mlds) of exceptional non-canonical pairs should satisfy the ascending chain condition (ACC). I will show the relationship of this conjecture with the termination of flips. This is a joint work with Jihao Liu.
李起峰(山东大学):Rigidity of projective symmetric manifolds of Picard number 1 associated to composition algebras
To each complex composition algebra A , there associates a projective symmetric manifold X(A) of Picard number 1. The vareity X (A) is closed related with Freudenthal's Magic Square, which is a square starting from the adjiont varieties of F_4, E_6, E_7 and E_8. In a
recent joint work with Yifei Chen and Baohua Fu, we obtain the deformation rigidity of X(A). In this talk, we will introduce the construction of X (A) from Freudenthal's Magic Square, the geometric properties of them, and finally the deformation rigidity of X(A).
孙笑涛(天津大学):Frobenius splitting of moduli spaces of parabolic bundles
Let C be a nonsingular projective curve over an algebraically closed field of characteristic p>0 and I\subset C be a finite set. If U_{C,ω} denotes the moduli space of semistable parabolic bundles of rank r and degree d on C with parabolic structures determined by ω=(k,{n(x),α(x)}_{x\in I}), we prove that U_{C,ω} is F-split for generic C and generic choice of I when p>3r.
谈胜利(华东师范大学):具有低斜率的叶层化代数曲面
代数曲面叶层化的最初研究要归功于庞加莱、潘勒维等人,他们用复代数几何研究微分方程,具体来说,就是利用参数曲线的几何理论研究一阶常微分方程,希望将参数曲线的拓扑性质、双有理不变量推广到微分方程。在停滞了100年后,受到森重文(S. Mori)的极小模型理论的影响,该研究重新引起了代数几何学家的注意。1987年,宫冈(Y. Miyaoka)首次将三维代数簇的极小模型理论引入到代数曲面叶层化的研究,证明典范除子不是伪有效的叶层化来自有理曲线纤维化,其它的叶层化的典范除子有查理斯基(Zariski)分解。30多年来,代数曲面纤维化的很多结果已经被推广到代数曲面叶层化,包括叶层化的奇点解消,典范除子和极小模型;小平维数与数值小平维数,以及非一般型叶层化的分类;叶层化的陈省身数、体积和斜率等不变量。我们将围绕肖刚斜率不等式在叶层化上的应用,介绍代数曲面叶层化研究的一些进展与未解决问题。
田志宇(北京大学):Deformation of stable maps via algebraic equivalence
I will describe a technique to lift algebraic equivalence of one cycles on smooth projective varieties to deformations between stable maps, and some of its applications in geometry and arithmetic. This is joint work with János Kollár.
杨南君(北京雁栖湖应用数学研究院):Milnor-Witt Motives and Bockstein Spectral Sequence
Chow-Witt group is the quadratic refinement of Chow group which applies to classifications of vector bundles, Hermitian K-theory and refined enumerative geometry. It is represented in the category of Milnor - Witt motives. In this talk, we analyze the MW-motives by Bockstein spectral sequence. We show its degeneracy for Grassmannian bundles, complete flag bundles and blowups.
张鼎新(清华大学):Compact Betti numbers of complex affine hypersurfaces
Given positive integers n<=m , and a complex polynomial f in n variables, how large the m-th compactly supported Betti number of the topological space (f=0)\subset C^n can be? I will sketch a non-optimal answer to this topological question using Frobenius actions on
rigid cohomology. The basic tools are two comparison theorems obtained jointly with Shizhang Li and with Daqing Wan. Joint work in progress with Daqing Wan.
周杨(复旦大学):A generaliation of mixed-spin-P fields
The theory of Mixed-Spin fields was introduced by Chang-Li-Li-Liu for the quintic threefold. Chang-Guo-Li has successfully applied it to prove famous conjectures on the higher-genus Gromov-Witten invariants. In this talk I will explain a generalization of the construction to more spaces. The key is the stability condition which guarantees the separatedness and properness of certain moduli spaces. It also generalizes the construction of the mathematical Gauged Linear Sigma Model by Fan-Jarvis-Ruan, removing their technique assumption about "good lifitings". This is a joint work with Huai-Liang Chang, Shuai Guo, Jun Li and Wei-Ping Li.
左康(武汉大学):Constructing rank-2 motivic local systems over the complex projective line removing 4 points via p-adic Hodge theory and Langlands correspondence
This is a joint work with Jinbang Yang. We construct infinitely many non-isotrivial families of abelian varieties of GL_2-type over the complex projective lines removing 4 points with bad reduction of type-(1/2)_infty via p-adic Hodge theory and Langlands correspondence. They lead to algebraic solutions of the Painleve VI equation. Recently Lin-Sheng-Wang proved a conjecture by Sun-Yang-Zuo on the torsioness of zeros of Kodaira-Spencer maps of those type families. Based on their theorem we show the set of those type families of abelian varieties is exactly parameterized by torsion sections of the universal family of elliptic curves modulo the involution.
同济大学数学科学学院,致远楼108报告厅



金方舟, 李灵光, 林胤榜, 张希平, 张子立, 朱子文
组织单位:同济大学数学科学学院
资助项目:科技部国家重点研发计划项目2021YFA1001400、国家自然科学基金青年项目12101455