
10 December 2022, Tongji University
丁之元Zhiyuan Ding
段炼Lian Duan
Daniel Skodlerack
涂君武JunWu Tu
张正Zheng Zhang
张子宇Ziyu Zhang
8:30-9:20 张正
9:30-10:20 段炼
10:30-11:20 涂君武
13:30-14:20 Skodlerack*
14:30-15:20 丁之元
15:30-16:20 张子宇
丁之元: On the determinant of cohomology of the universal Drinfeld shtuka
We compute the determinant of cohomology of the universal Drinfeld shtuka. We first prove a vanishing theorem for shtukas, which implies that the determinant of cohomology is canonically trivial away from the horospherical loci. Then we use deformation theory to compute its divisor explicitly. As an application, we construct certain rational functions on the moduli stack, which are analogues of the classical modular units.
段炼: On the torsion-finiteness of abelian varieties over torsion extensions
It is well known that over any number field, the Mordell Weil group of an abelian variety is finitely generated. Thus an abelian variety has only finitely many rational torsion points over a number field. This is in general not true if the base field is an infinite extension over Q. However, around 1981 Ribet proved that every abelian variety defined over a number field still has only finitely many torsion Q^ab-points, where Q^ab is the maximal abelian extension of Q. His result is then generalized by the works of Zarhin, Lombardo, and Rossler-Szamuely. In this talk, we will introduce another generalization of this result. That is, we will study the "torsion-finiteness" of an abelian variety over an infinite extension of the base field generated by adjoint all the torsion points of another abelian variety. Assuming the Mumford-Tate conjecture, we will give a criterion to the torsion-finiteness in terms of the Mumford-Tate groups of the related abelian varieties. In particular, when the conjecture is known, our theorem will deduce the unconditional results. This includes most cases of abelian varieties of dimension <=3 and the CM cases. This is a joint work with Jeff Achter and Xiyuan Wang.
Daniel Skodlerack: Irreducible representations of quaternionic forms of p-adic classical groups and beta-extensions
Beta-extensions are the positive level part for Bushnell-Kutzko-Stevens-types for cuspidal representations for p-adic classical groups. They also play a role in the classification of non-cuspidal representations. But here in opposite to the quasi-split case one needs to be more careful in choosing a beta-extension for a quaternionic form of a classical group. I will give an overview about beta-extensions and their construction and then present which ones are suitable for quaternionic forms.
涂君武: From categories to birational invariants of Calabi-Yau 3-folds
In this talk, we shall discuss categorical enumerative invariants and their Morita invariance. In this case of Calabi-Yau 3-folds, these are new birational invariants. Conjecturally, they agree with partition functions in topological string theory. We also discuss its variational structures.
张正: Cubic threefolds with an involution and their intermediate Jacobians
We study the moduli space of cubic threefolds admitting an involution via the period map sending such a cubic threefold to the invariant/anti-invariant part of the intermediate Jacobian. Our main result is global Torelli holds for the period map. Key ingredients of the proof include a description of the invariant/anti-invariant part of the intermediate Jacobian as a Prym variety and a detailed study of certain positive dimensional fibers of the corresponding Prym map. The proof also relies on the results of Donagi-Smith, Ikeda and Naranjo-Ortega on related Prym maps. This is joint work with S. Casalaina-Martin and L. Marquand.
张子宇: Semi-continuity in variation of GIT
We review the classical semi-continuity theorem in geometric invariant theory, and generalize it to the relative case with semi-ample polarizations. The proof relies on two main ingredients, namely continuity of the M-function and finiteness of possible choices of semi-stable loci. The application of semi-continuity in the study of degenerations of Hilbert schemes will also be mentioned if time permits. Based on joint work with Lars Halle and Klaus Hulek.
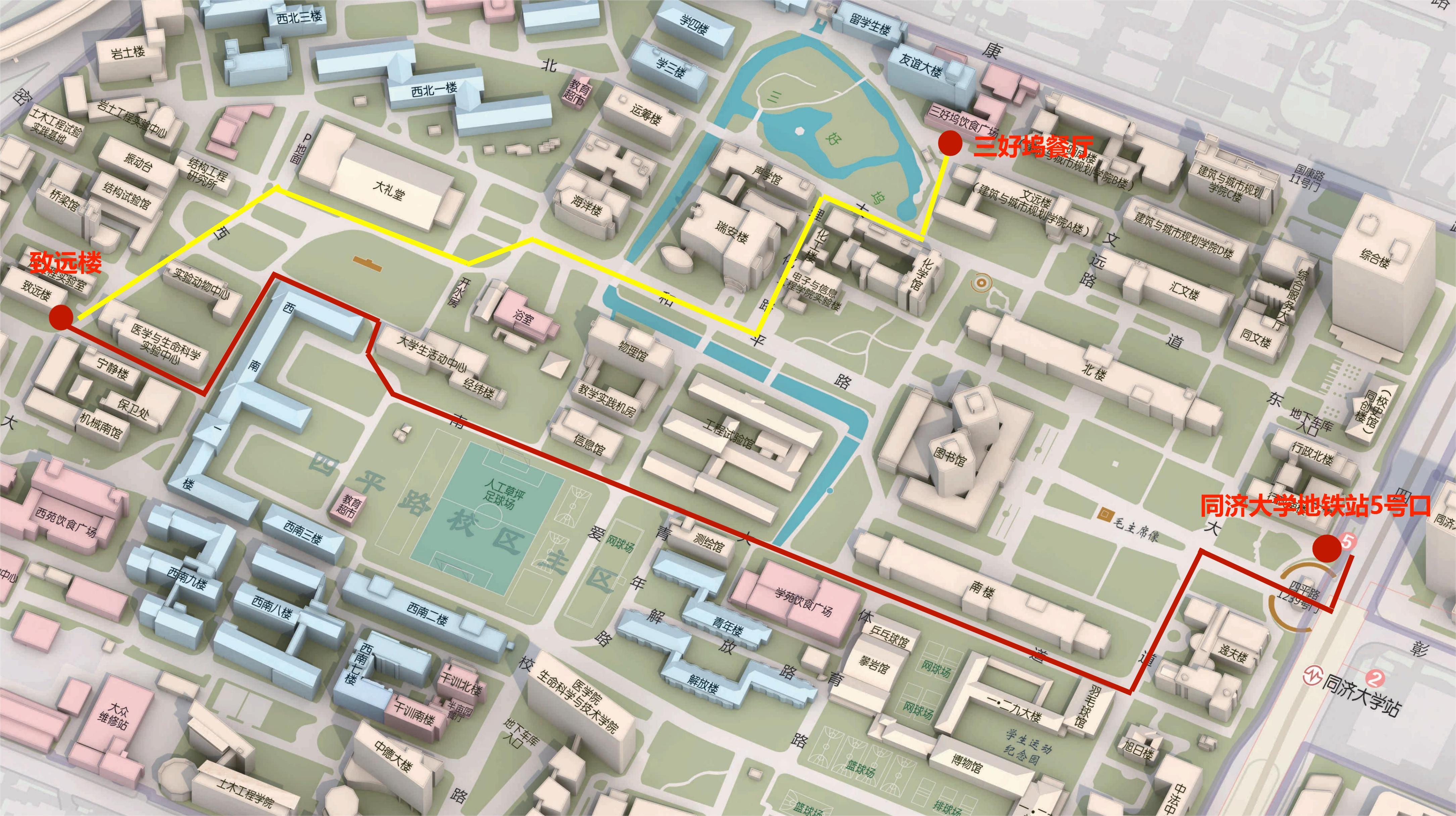
The talks will take place at Room 108 Zhiyuan Building (致远楼108), Tongji University.


Fangzhou Jin, Lingguang Li, Yinbang Lin, Xiping Zhang, Zili Zhang, Ziwen Zhu
This workshop is hosted by the School of Mathematics of Tongji University under the support of the National Key Research and Development Program of China Grant Nr.2021YFA1001400.