
27-28 November 2021, Tongji University
杜荣Rong Du (ECNU)
高云Yun Gao (Shanghai Jiaotong University)
胡勇Yong Hu (Shanghai Jiaotong University)
江辰Chen Jiang (Fudan University)
江智Zhi Jiang (Fudan University)
李志远Zhiyuan Li (Fudan University)
罗马Ma Luo (ECNU)
吕鑫Xin Lv (ECNU)
徐万元Wanyuan Xu (Shanghai Normal University)
张通Tong Zhang (ECNU)
张子宇Ziyu Zhang (ShanghaiTech University)
9:15-9:30 Opening
9:30-10:30 杜荣
10:30-10:45 Group Photo
11:00-12:00 张子宇
14:00-15:00 吕鑫
15:15-16:15 徐万元
16:30-17:30 罗马
8:30-9:30 张通
9:45-10:45 胡勇
11:00-12:00 高云
14:00-15:00 江智
15:15-16:15 江辰
16:30-17:30 李志远
杜荣: Vector Bundles on Fano varieties
Abstract: We will introduce the background of algebraic vector bundles on special Fano varieties and some open problems related to them in algebraic geometry.
高云: Dimension estimate, HJY Gap conjecture and SOS conjecture
Abstract: In this talk, we will introduce a dimension formula for local holomorphic mappings. This formula gives a dimension estimate for the linear spans of the images of linear subspaces. As an application, we use this formula to study the holomorphic mappings between real hyperquadrics, especially, Huang-Ji-Yin Gap Conjecture and sum of squared Conjecture. We partly solve these two conjectures and extend them to more general cases. This is a joint work with Sui-Chung Ng.
胡勇: Noether-Severi inequality and equality for irregular threefolds of general type
Abstract: We prove the optimal Noether-Severi inequality that $\vol(X) \ge \frac{4}{3} \chi(\omega_{X})$ for all smooth and irregular $3$-folds $X$ of general type over $\CC$. This answers an open question of Z. Jiang in dimension three. For those $3$-folds $X$ attaining the equality, we completely describe their canonical models and show that the topological fundamental group $\pi_1(X) \simeq \ZZ^2$. This is a joint work with Tong Zhang.
江辰: Explicit boundedness of canonical Fano 3-folds: known results and open problems
Abstract: Motivated by the classification of canonical Fano 3-folds, we are interested in boundedness results on diffrent kinds of canonical Fano 3-folds, such as anticanonical systems, indices, degrees, and so on. I will summarize known results with some progress (based on joint works with Meng Chen and Yu Zou) and open problems in this area.
江智: Basepoint freeness thresholds of polarized abelian varieties
Abstract: We will explain the connection between basepoint freeness threshold and syzygies of abelian varieties. If time permits, we will also explain several ways to estimate the basepoint freeness threshold.
李志远: Finiteness problem for hyperkähler varieties
Abstract: The finiteness theorem for curves and abelian varieties, such as Mordell conjecture and Shafarevich conjecture are well-known. Recently, there is a series study of various Shafarevich’s finiteness conjectures for K3 surfaces. In this talk, I will talk about finiteness result for hyperkähler varieties. This includes a proof of the finiteness of birational classes of hyperkähler varieties satisfying Shafarevich’s condition . Our method also confirms Shafarevich’s finiteness conjecture (on geometric Picard lattices) in the CM case. The later conjecture can be viewed as a strengthen of the Vojta-Lang conjecture. This is a joint work with Lie Fu and Haitao Zou.
罗马: Periods and completions of fundamental groups
Abstract: To study periods of fundamental groups, one needs to linearize these discrete groups and consider their various completions, such as unipotent completions and relative completions. In this talk, we discuss what these completions are and how they are related to the study of motives and their periods. In particular, the focus will be put on the cases of projective lines and elliptic curves.
吕鑫: Strict Arakelov inequality for a semi-stable fibration
Abstract: For a semi-stable non-birationally isotrivial family of n-folds over a smooth projective curve, we show that the Arakelov inequality for the direct image of the v-th relative canonical sheaves is strict when v is large enough. This is a joint work with Jinbang Yang and Kang Zuo.
徐万元: Strict Arakelov type inequalities for fibered surfaces
Abstract: For a family of non-isotrivial semistable varieties of general type, we have the well known Viehweg-Zuo's Arakelov inequality for the slope of the pushforward of the relative pluricanonical sheaf. In this talk, I shall talk about the strictness of the Arakelov inequality for fibered surfaces. We also generalize it to the non-semistable case and to the positive characteristic case. This work is in progress.
张通: Relative Clifford inequality for families of curves
Abstract: The Clifford inequality is a fundamental result in the study of geometry of algebraic curves. In this talk, I will present a generalization of this inequality for a family of curves, and such a generalization will give some new numerical inequalities regarding the geometry of higher dimensional varieties.
张子宇: Examples of stable bundles on hyperkähler manifolds of higher dimensions
Abstract: Stable sheaves on K3 surfaces have been extensively studied. However, it is a challenging question to construct non-trivial examples of stable sheaves on hyperkähler manifolds of higher dimensions. Applying techniques in derived categories, I will present several constructions, which produce irreducible components of the moduli spaces of such sheaves. Based on joint work with Fabian Reede.
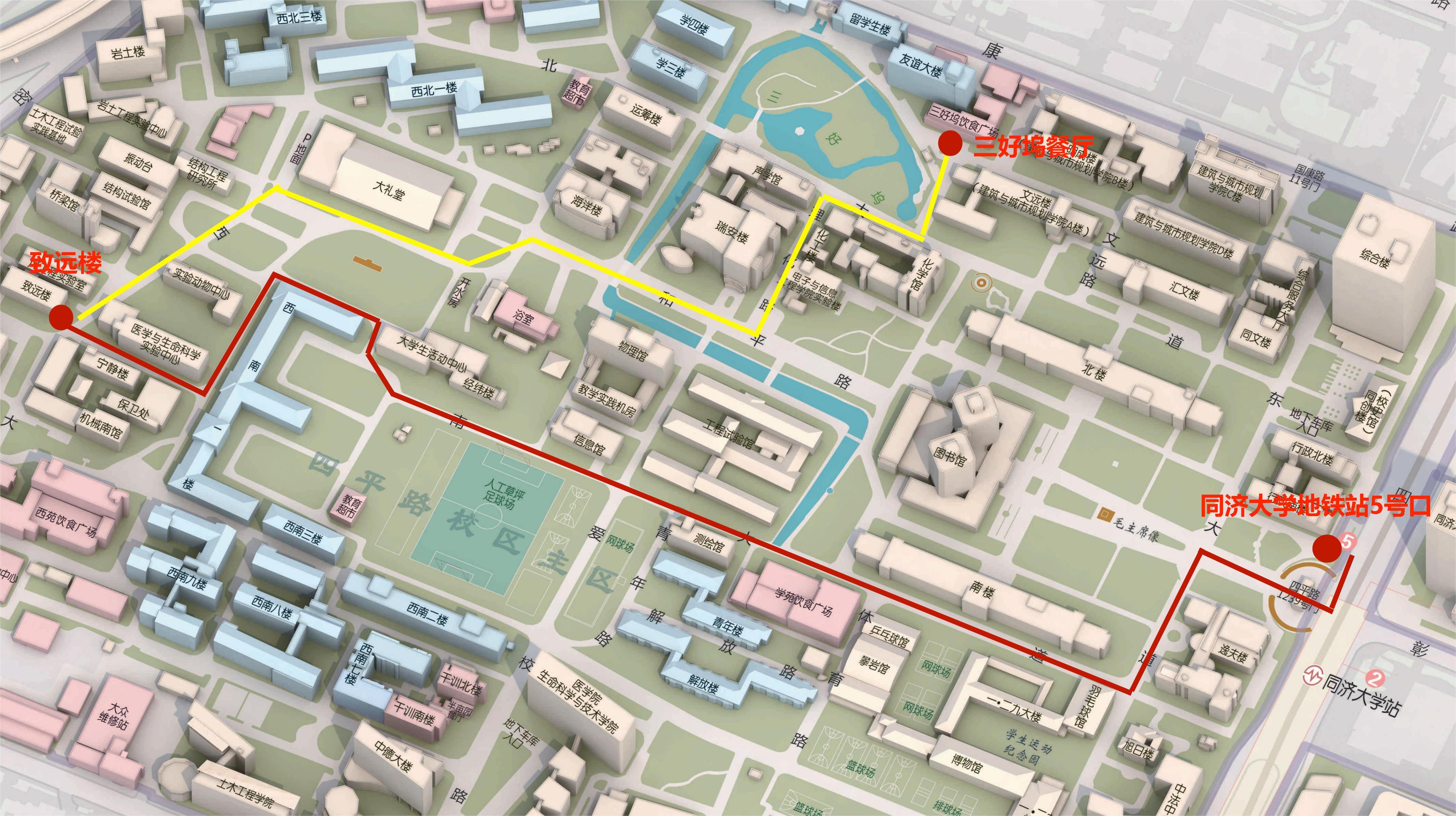
The talks will take place at Room 108 Zhiyuan Building (致远楼108), Tongji University.


Fangzhou Jin, Lingguang Li, Yinbang Lin, Xiping Zhang, Zili Zhang
This workshop is hosted by the School of Mathematics of Tongji University.