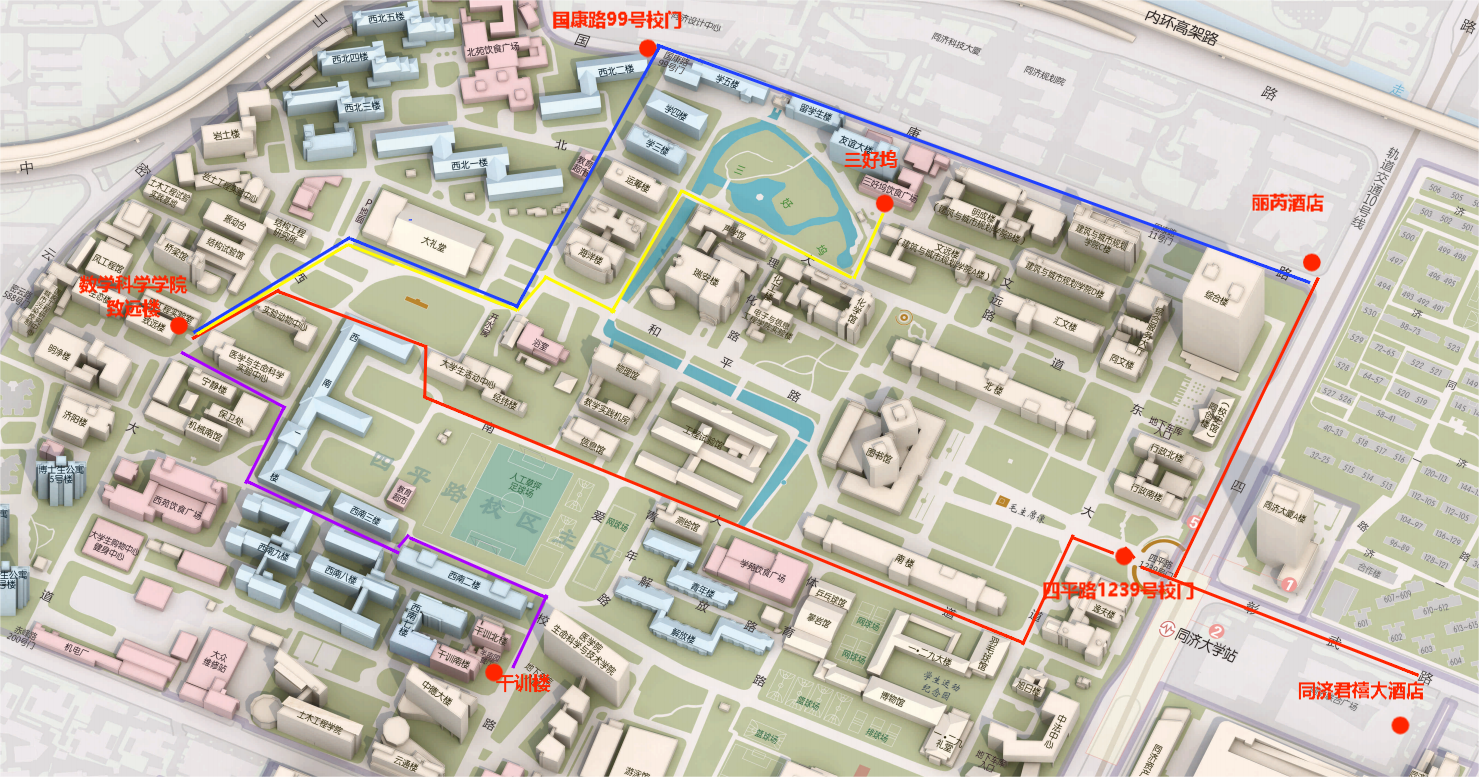
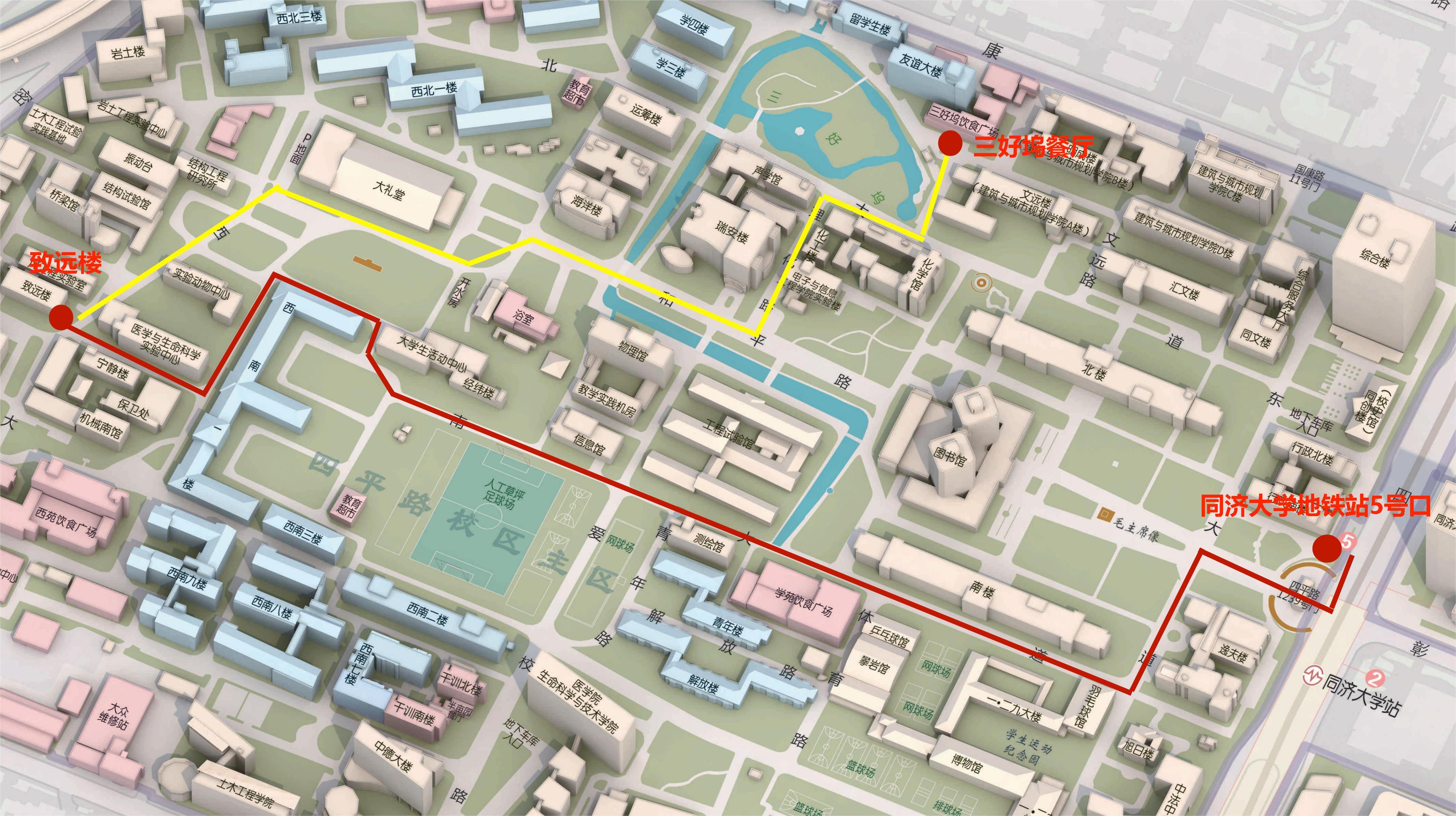

2023年12月8-11日, 同济大学数学科学学院
郭靖邦(复旦大学)
胡勇(南方科技大学)
李铎(中山大学珠海)
梁永祺(中国科学技术大学)
王善文(中国人民大学)
訚琪峥(北京大学)
张鼎新(清华大学)
张磊(中山大学珠海)
周子浚(上海交通大学)
宗润弘(南京大学)
12月8日
报到
12月9日
9:30-10:30 胡勇
10:45-11:45 梁永祺
合影
午餐
14:00-15:00 张磊
15:15-16:15 王善文
16:30-17:30 郭靖邦
晚宴
12月10日
8:30-9:30 訚琪峥
9:45-10:45 宗润弘
11:00-12:00 李铎
午餐
14:00-15:00 周子浚
15:15-16:15 张鼎新
12月11日
自由讨论
郭靖邦: Topological Hochschild homology and Prismatic Cohomology
The theory of prismatic cohomology is a universal p-adic cohomology theory, in the sense that it specializes to the classical p-adic cohomology theories such as the de Rham cohomology and the p-adic etale cohomology. Originally, this universal p-adic cohomology theory was expected by the calculation of topological Hochschild homology for (integral) perfectoid rings.
In this talk, the basic ideas of topological Hochschild homology will be introduced, and the construction of the motivic filtrations, whose associated graded pieces are given by the (variants of) prismatic cohomology, will be exhibited. If time permits, a calculation of topological cyclic homology of local fields through the descent technique, which reflects the idea of covering the Cartier-Witt by the Breuil-Kisin, is to be discussed.
胡勇: Strong Approximation and Integral Quadratic Forms over Affine Curves
In the classical arithmetic theory of quadratic forms over global fields, strong approximation and the Hasse principle play a very important role. In this talk, we discuss extensions of some results in this direction to function fields of curves defined over more general fields. In particular, we give examples where strong approximation and the Hasse principle for integral quadratic forms hold, and examples where they do not hold. This is based on a joint work in progress with Jing Liu 刘靖 and Yisheng Tian 田乙胜.
李铎: Some remarks on Kumar's conjecture
Recently Kumar propose a conjecture about morphisms between rational homogeneous varieties. In principal, he conjectures there is only constant morphisms from X to Y if the ssrank of X is bigger than the ssrank of Y. We will discuss some recent progress and some applications about this problem.
梁永祺: 奇亏格超椭圆曲线的局部整体原则
Scharaschkin和Skorobogatov等人猜测Brauer-Manin障碍是定义在数域上的射影光滑曲线上的有理点不满足局部整体原则的唯一障碍。对于任意数域和任意给定除4余1的自然数g,我们具体构造出一族(单参数的)亏格为g的由Brauer-Manin障碍解释的局部整体原则失效的曲线。我们的结论为上述猜想给出了具体的例证。这是我和博士生黄凯最近的工作。
王善文: p-adic one variable functions and representations of GL_2(Q_p)
In this talk, we will explain our extension of the dictionary between Fontaine rings and p-adic functionnal analysis, and a refinement of the p-adic local Langlands correspondence for principal series representations of GL2(Qp). This is joint work with Pierre Colmez.
訚琪峥: Abelian fibrations, Perverse = Chern, and multiplicativity
The perverse filtration captures interesting homological information of algebraic maps. Recent studies of the Hitchin and Beauville-Mukai integrable systems suggest two common features of the perverse filtration for abelian fibrations:
1) the perverse filtration is multiplicative with respect to the cup product;
2) the perversity of tautological classes is governed by the Chern degree.
In this talk, I will explain a unified approach to both statements for a natural class of abelian fibrations, namely fibrations in compactified Jacobians. As a consequence of our theory, we obtain a new, geometric proof of the P = W conjecture for GL_n. Joint work with Davesh Maulik and Junliang Shen.
张鼎新: An Ax-Katz type theorem for irreducible hermitian symmetric spaces
For a subvariety X of P^n over a finite field k of characteristic p, the classical Ax-Katz theorem gives an upper bound for the p-order of Card X(k) - Card P^n(k), in terms of the degrees of defining polynomials of X. I shall present a generalization of this theorem, with P^n replaced by any irreducible hermitian symmetric space.
张磊: Frobenius Descent and Drinfeld's Lemma for Stacks
Drinfeld's lemma for schemes and diamonds plays a very important role in both equal and mixed characteristic Langlands. A key ingredient of Drinfeld's lemma is the "permanence property" of certain algebro-geometric objects, meaning that the étale fundamental groups of those algebro-geometric objects are stable under base change of algebraically closed fields. The permanence property in the positive characteristic case is a consequence of a descent phenomenon called "Frobenius descent". In this talk, we'll establish the Frobenius descent for general fibered categories over finite fields. A direct consequence of this is a version of Drinfeld's lemma for algebraic stacks. We will also give some other applications of this result. This is joint work in progress with Valentina Di Proietto and Fabio Tonini.
周子浚: Coulomb branch and enumerative geometry
Coulomb branches of 3d N=4 theories and their quantizations, originated in physics and later developed by Braverman-Finkelberg-Nakajima, provide new geometric ways of constructing algebras and their representations. In this talk, I will discuss its connection to enumerative geometry, where representations of Coulomb branches are expected to show up in the moduli of quasimaps into Higgs branches (i.e. GIT quotients). Interesting enumerative invariants, such as I-functions/Okounkov's vertex functions, quantum differential/difference modules, etc. can be described in terms of quantized Coulomb branch. In the case of holomorphic symplectic quotients T^*N///G, we also need to introduce a virtual variant of the Coulomb branch, where the convolution product is modified by a virtual intersection. Applications include variation of GIT and 3d abelian mirror symmetry.
宗润弘: New anabelian phenomena for curves in positive characteristic
In the 1980s, in his famous letter to Faltings, Grothendieck suggested a theory which he called "anabelian geometry". This theory aims to reconstruct algebraic varieties from their algebraic fundamental groups (e.g. étale, tame, etc.). In the particular case of curves, Grothendieck's anabelian philosophy has provided a blueprint for the development of anabelian geometry (especially, for curves over arithmetic fields of characteristic 0)and has continuously guided the advancement of the theory until today.
In this talk, I will first outline some historical background and explain some key results, particularly emphasizing the significant contributions to anabelian geometry made by the Japanese school led by S. Mochizuki and A. Tamagawa. Following that, I will introduce a completely new anabelian phenomenon concerning curves in positive characteristic. This phenomenon is the first anabelian phenomenon that cannot be explained by using Grothendieck's original anabelian philosophy. Moreover, further study of this phenomenon provides an important basis for constructing a general theory for anabelian geometry of curves over algebraically closed fields of characteristic p.
This is a joint work with Zhi Hu (NJUST, Nanjing) and Yu Yang (RIMS, Kyoto).
同济大学数学科学学院,致远楼108报告厅



金方舟, 李灵光, 林胤榜, 张希平, 张子立, 朱子文
组织单位:同济大学数学科学学院
资助项目:科技部国家重点研发计划项目2021YFA1001400、国家自然科学基金青年项目12101455